¿Qué son las Curvas de nivel en Topografía?

¿Qué son las curvas de nivel en topografía?: Las curvas de nivel son el método cartográfico más común para representar la altitud de la superficie. A partir de las curvas de nivel la variable Z del terreno se puede expresar como un plano bidimensional.

Una curva de nivel es aquella línea que en un mapa o imagen une todos los puntos que tienen igualdad de condiciones y de altura. Existen varias convenciones para la representación de estas curvas, pero actualmente los formatos estandarizados son los formatos vectoriales. Estos son utilizados en una gran variedad de escalas y aplicaciones.

Los usos en la ingeniería son variados, pero específicamente para la ingeniería civil se las utiliza para conocer la estructura topográfica de un lugar destinado para la construcción. curvas de nivel en topografía

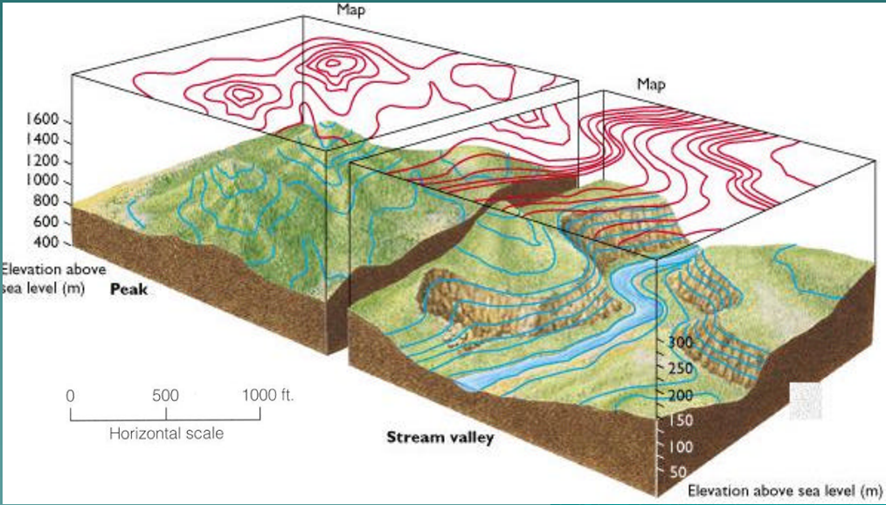
Aplicaciones de las curvas de nivel:

Una vez elaborado el mapa topográfico con la representación grafica del relieve del terreno por medio de las curvas de nivel, podemos utilizar el mismo de diferentes maneras en la planificación y ejecución de obra civiles.

Un mapa topográfico bien elaborado constituye una base de información indispensable en la planificación, ejecución y control de todo proyecto.

De un mapa topográfico con curvas de nivel podemos determinar la cota o elevación de cualquier punto sobre el plano, la pendiente entre dos puntos, estimar los volúmenes de corte y relleno de material requerido en la ejecución de una obra, proyectar razado de vías, etc. Curvas de nivel en topografía

• Trazado de líneas de pendiente constante

Un procedimiento común en el estudio de rutas para proyectos viales, ferroviarios, etc. es el de trazado de líneas de pendiente constante. En la escogencia de la ruta de una carretera en terreno ondulado o de montaña, una de las mayores limitantes es el de mantenerse dentro de los límites de pendiente y longitudes criticas establecidos por el comportamiento de vehículos pesados, por lo que se hace necesario establecer un procedimiento para trazar, a partir de un mapa de curvas de nivel, una línea de pendiente constante que no sobrepase la pendiente máxima permitida según el tipo de carretera.

• Calculo de la cota de un punto

Comúnmente, en la elaboración de proyectos, es necesario determinar la cota de un punto sobre un mapa de curvas de nivel.

• Perfiles longitudinales

En un proyecto de ingeniería, por lo general es necesario analizar diferentes alternativas, por lo que sería impráctico levantar en campo un perfil para cada una de las alternativas planteadas. El perfil longitudinal es la traza que el eje del proyecto marca sobre el plano vertical. Un perfil longitudinal se puede construir a partir de las curvas de nivel.

¿Qué son las curvas de nivel y cómo se dibujan?

Las curvas de nivel son líneas imaginarias trazadas en un plano cartográfico que conectan puntos con la misma altitud sobre el nivel del mar. Estas líneas permiten representar la topografía de un terreno tridimensional en un formato bidimensional, mostrando su forma, pendientes, elevaciones y depresiones.

Ejemplo

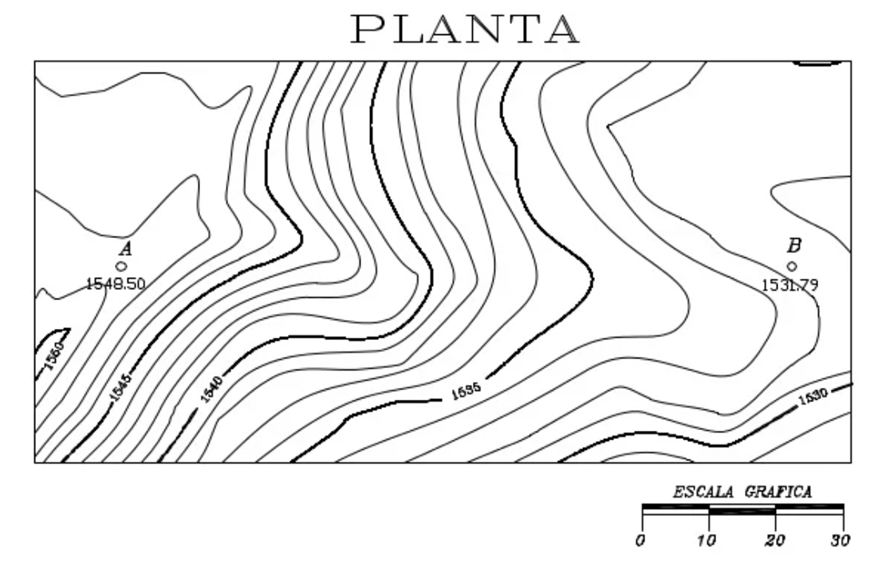
Construya el perfil longitudinal del alineamiento AB a partir de la figura

Solución

• Determinamos, mediante el proceso de interpolación descrito anteriormente, las cotas de los puntos A (QA = 1548.50) y B (QB = 1531.79).
• Luego trazamos un sistema de coordenadas rectangulares x, y en donde se representará el perfil longitudinal del alineamiento AB.
• Como por lo general, los desniveles a representar son mucho menores que las distancias horizontales, se acostumbra que la escala del eje de las cotas sea unas diez veces mayor que la escala de las distancias. En nuestro ejemplo, por problemas de espacio, usaremos la misma escala horizontal del mapa 1:1000, y una escala vertical 1:200 para las cotas.
• Determinamos las distancias parciales entre cada uno de los puntos de intersección de la línea AB con las curvas de nivel. Como la escala horizontal del mapa es la misma que la del perfil, bastara con proyectar los puntos de intersección sobre el eje horizontal del perfil.
• Las cotas de los puntos de intersección corresponden a las cotas de las curvas de nivel intersecadas.
• Unimos en forma consecutiva los puntos ploteados obteniendo el perfil longitudinal AB.
• Por lo general en la parte inferior se colocan en forma tabulada las distancias parciales, progresivas y las cotas del terreno.

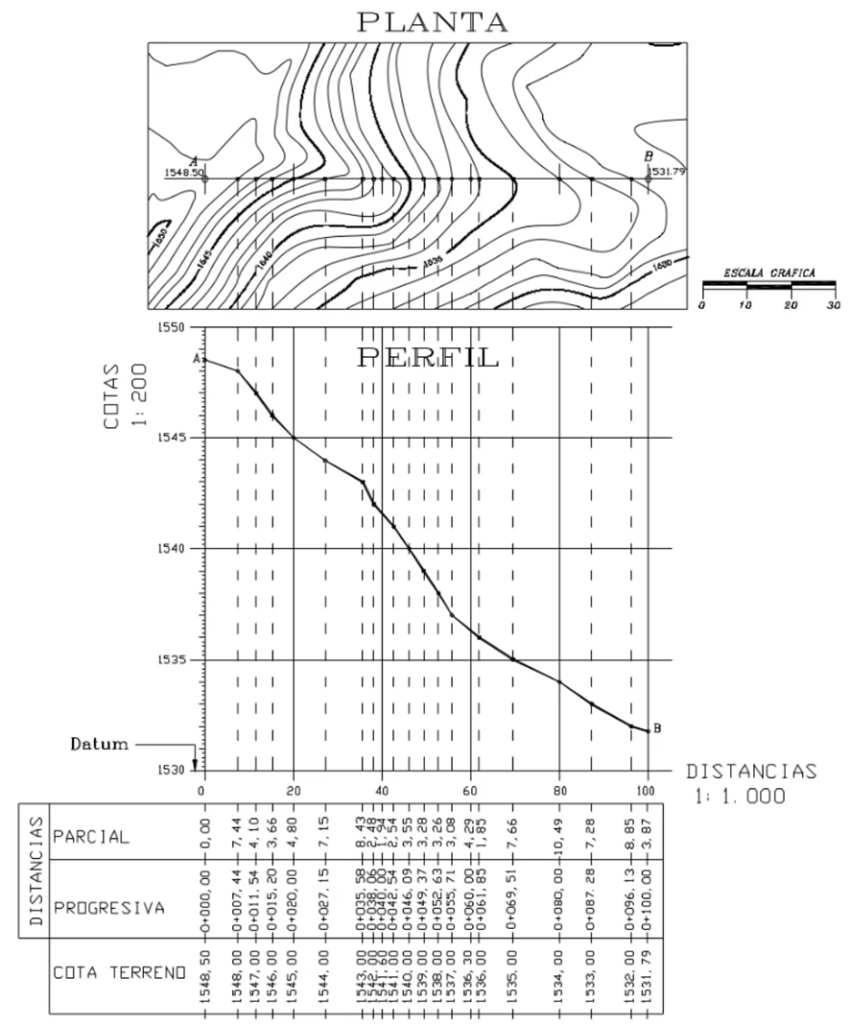
¿Qué son las curvas de niveles y qué son las cotas?

Las curvas de nivel y las cotas son conceptos fundamentales en topografía, cartografía y diseño de terrenos. A continuación, te explico cada uno:

Curvas de Nivel

Son líneas imaginarias dibujadas en un plano topográfico que unen puntos con la misma altitud sobre el nivel del mar o sobre una base de referencia específica. Representan la forma y la elevación del terreno en dos dimensiones.

Características principales:

1. Equidistancia: La separación entre curvas consecutivas, conocida como equidistancia, es constante y depende de la escala del plano y de las características del terreno.
2. Representación del relieve:
   • Curvas cercanas: Indican pendientes pronunciadas.
   • Curvas separadas: Representan pendientes suaves o zonas planas.
3. Forma: La disposición de las curvas muestra la forma del terreno (valles, colinas, montañas, etc.).
4. Cierre: Las curvas siempre forman un circuito cerrado, aunque a veces esto no es visible dentro de la zona mapeada.

Aplicaciones:

• Diseño de proyectos de construcción, como carreteras y presas.
• Análisis de pendientes y drenaje.
• Planeamiento agrícola y urbano.

---

Cotas

Las cotas son valores numéricos que indican la altitud de un punto específico respecto a un nivel de referencia, generalmente el nivel del mar. Se expresan en unidades de longitud (metros o pies).

Tipos de cotas: Curvas de nivel en Topografía

1. Cotas absolutas: Son las elevaciones medidas desde el nivel del mar.
2. Cotas relativas: Se miden respecto a un nivel base local definido para un proyecto específico.

Aplicaciones:

• Marcar puntos específicos en un plano (e.g., la altura de un terreno, nivel de una losa o el fondo de una zanja).
• Comparar diferencias de elevación entre puntos.
• Generar perfiles y secciones transversales.

---

Relación entre Curvas de Nivel y Cotas

Las curvas de nivel permiten una visualización continua del relieve, mientras que las cotas aportan información numérica precisa en puntos concretos. Por ejemplo, en un plano topográfico, las curvas muestran el terreno general, y las cotas destacan las elevaciones exactas en puntos clave como intersecciones o cumbres.

Ambos conceptos son esenciales en la ingeniería, arquitectura y geografía para diseñar, analizar y construir con precisión.